Excel Hacks : How to copy data in row of excel into a column (Transpose)

Working on a data science project makes you play with diverse data sources in the most crazy way you can imagine.

While aligning the data programmatically via data frames in the most sane way to do, but sometime you just want to check the data in a quick dirty way via the all familiar Excel.

Aligning the data in one format (vertically or horizontally) can be a challenge though, since there is no universal rule for defining what should be on X axis and what should be on Y. There is one trick though you can use to quickly transpose the numbers either way (vertical to horizontal or vice versa)

1. Copy the data, say which is present in the horizontal format.



2. Go the sheet now where you want to paste this in the vertical format, right click on cell where you want data to start from, right click, and from Paste options choose Transpose option.



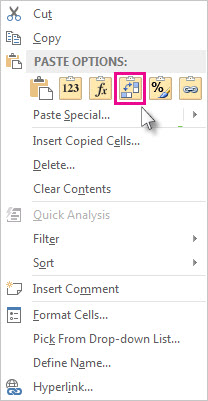
3. You will have the data in the format you want.

Having multiple rows in Bookmarks Toolbar in Firefox

I have recently been bookmarking a lot, I guess that happens when teams are busy doing surveys and are not quite sure of right direction but have tonnes of material to refer to, or probably you are picking a domain, worst still may be both :)

Anyways thing is you may end up with too many bookmarks and folders to be contained in a single line. Is there a way you can still see all your bookmarks and folders?

Just discovered this wonderful plugin, which basically does css adjustments allowing bookmark line to span to multiple lines.

So this




Turns into



So if you are on firefox, do give a try for sure. Here is the link
https://addons.mozilla.org/en-US/firefox/addon/multirow-bookmarks-toolbarplus/